Physics rule
Physics rule

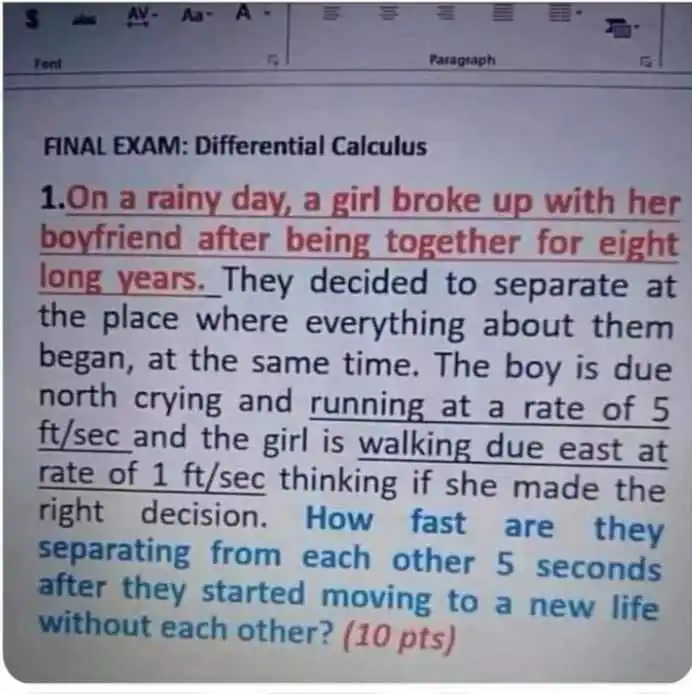
Physics rule


They're traveling away from their origin at constant velocities, so they're traveling relative to each other at constant velocities as well.
The magnitude of the resulting vector (i.e., speed) can be calculated trivially since their movement is perpendicular on a plane, as the root of sum of squares, which many could recognize as the Pythagorean theorem:
√((5 ft/s)² + (1 ft/s)²) = √26 ft/s ≈ 5.1 ft/s
You can verify this by finding that their average speed apart is the same at all times (for all t > 0):
Vavg = √((t * 5 ft/s)² + (t * 1 ft/s)²) / t = √(t² * ((5 ft/s)² + (1 ft/s)²)) / t = √26 ft/s
Don't forget to calculate the location where everything about them began and then include the curvature of Earth considering the latitude of said location into your speed calculation.
No, they're spherical children in a vacuum.
https://en.m.wikipedia.org/wiki/Spherical_geometry
I couldn't find 'potatoy geometry' for a better approximation of earth.
You'll note that I already assumed that they were on a plane, not the surface of a sphere.
It's been a while, but I think it's quite trivial.
After one second, they span a right angled triangle, therefore (using a² + b² = c²) their distance is √(5²+1²) = ~5.1 ft
They move at constant speed, therefore they seperate at 5.1 ft/s. That means at 5s it's just 5.1 × 5 = 25.5 ft for the distance and their speed is still the same.
They each move at a constant speed, but the distance between them doesn't increase at a constant pace. See my other comment.
Edit: I am dumb, and looked at the wrong number.
I'm trying to apply the most simple math possible and it seems to add up.
After one second, their distance is √(5² + 1²) = ~5.1 ft
After two seconds, their distance is √(10² + 2²) = ~10.2 ft
After three seconds, it's √(15² + 3²) = ~15.3 ft
As speed is the rate of change of distance over time, you can see it's a constant 5.1 ft/s. You're free to point out any error, but I don't think you need anything more than Pythagoras' theorem.
The question specifically asks for their seperation speed at 5s to ignore any initial change in their speed as they first need to accelerate, I'd assume.
I don't see why the distance between them isn't growing at a constant speed.
At any given time t seconds after separation, the boy is 5t north, and the girl is 1t east. The distance between them is defined by the square root of ((5t)2 + (t)2 ), or about 5.099t.
In other words, the distance between them is simply a function defined as 5.099t, whose first derivative with respect to time is just 5.099.
Depends on where they met each other. If they for example fell in love during the main event of a trip to the north pole, that would change things a lot.
there is no north at the north pole so actually that's the one place it can't be
If you're at the south pole, would every direction count as north?
Sure, but there is a north say 30 ft away from the north pole.
Its pretty convenient that its raining, which means you can ignore the coefficient of friction since the surface is slippery
It's* pretty convenient that it's* raining
Differential calculus? That looks more like algebra. Their speed is constant.
I agree, it is not calculus, it's trigonometry.
Each of their speeds is constant, but different, and they're walking in different directions.
Their distance is the hypotenuse of a triangle with sides 5t and t which will be root((5t)2 + t2). So the distance at time t of the ex lovers will be root(26) × t. You can basically grasp intuitively that the speed is indeed constant and equals to the root(26)=5.1 ft/sec. Technically you’d use the derivative power rule to drop the t and get the speed.
Look. Teachers have some unresolved shit as well.
It doesn't matter what the actual answer is; to both the boy and the girl it feels like C.
reminds me of that one song, proof that geometric construction can solve all love affairs or something like that
what
Who hurt the math teacher?
9,14 Meter
The question states "how fast", not "how far", thus you need to give the acceleration at that moment.
At t=0, the boy and girl both haven't moved, so their positions are 0. The distance between them is also 0, as is their acceleration.
The boy's distance in meters is t1.524, the girl's distance is t0.3048. The distance between them is sqrt( b2 \* g2 ). The velocity is the current distance minus the previous distance.
At t=1, b=1.524m, g=0.305, d=sqrt( g2 \* g2 )=0.465, v=d-d^(t-1)=0.465m/s.
At t=5, b=7.62, g=1.524, d=11.613, and v=4.181m/s.
Edit: fixed markdown
Velocity is not the difference between distances.