This feels wrong. I love it.
This feels wrong. I love it.
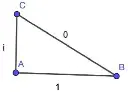
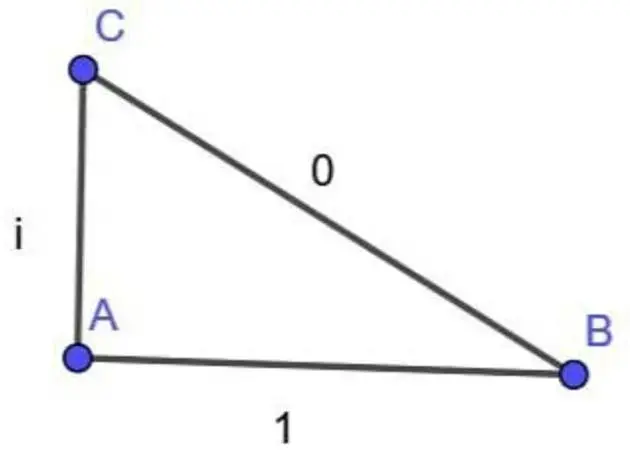
This feels wrong. I love it.


You're viewing a single thread.
This is pretty much the basis behind all math around electromagnetics (and probably other areas).
Would you explain how, for a simpleton?
The short version is: we use some weird abstractions (i.e., ways of representing complex things) to do math and make sense of things.
The longer version:
Electromagnetic signals are how we transmit data wirelessly. Everything from radio, to wifi, to xrays, to visible light are all made up of electromagnetic signals.
Electromagnetic waves are made up of two components: the electrical part, and the magnetic part. We model them mathematically by multiplying one part (the magnetic part, I think) by the constant i, which is defined as sqrt(-1). These are called "complex numbers", which means there is a "real" part and a "complex" (or "imaginary") part. They are often modeled as the diagram OP posted, in that they operate at "right angles" to each other, and this makes a lot of the math make sense. In reality, the way the waves propegate through the air doesn't look like that exactly, but it's how we do the math.
It's a bit like reading a description of a place, rather than seeing a photograph. Both can give you a mental image that approximates the real thing, but the description is more "abstract" in that the words themselves (i.e., squiggles on a page) don't resemble the real thing.
Makes sense, thanks. More of a data transmission than an electrical power thing.
Yeah, it's about how electromagnetic energy travels through space.
Thanks!
I remember the first time we jumped into the complex domain in an electronics course to calculate something that we couldn’t reach with the equations we had so far.
… and then popping out the other side with a simple (and experimentally verified) scalar, after performing some calculation in the complex domain, using, bafflingly, real world inputs.
I suddenly felt like someone from the future barged into my Plato’s cave and proceeded to perform some ritual.
Like I know what’s happening, I’ve done these calculations before, but seeing them used as an intermediate step in something real in the real world was pretty cool!
Did not prepare me for all the Laplace et al shenanigans later. Did I test well in those courses? No. Did I have the most fun building the circuits regardless? You bet.
Oh to be a student again. Why are real world jobs so boring.
Circles are good at math, but what to do if you not have circle shape? Easy, redefine problem until you have numbers that look like the numbers the circle shape uses. Now we can use circle math on and solve problems about non-circles!
Yes, relativity for example!