Skip Navigation

You're viewing part of a thread.

Show Context
574 comments

  • Nothing in Maths is made up. It’s based on our observations of how things work.

    The notation and syntax of how we express that, is made-up. There's multiple options. There's disagreements. Fuck me sideways, you are a teacher, and you can't figure out how being off-topic works?

    Evidently not, as you flip between 'this particular notation is the notation!' to 'of course other notations exist' and suffer zero cognitive dissonance. By capital-M "Maths," do you mean the notation on paper, or the underlying laws-of-reality stuff? It depends! It's ambiguous and requires context, or maybe you're just factually wrong at least one of those times, and either way, that means it's plainly not THE SAME KIND OF THING as the laws-of-reality stuff.

    It's a category error. You can prove that the word prove isn't spelled proove, for some reason, but the heavens would not bend the other direction if that changed. We could swap square braces and parenthesis and nothing would be different. We could use the glyph "&" instead of "7." These details are mutable and completely fucking arbitrary. But then & - 6 = 1, and you could never proove otherwise.

    Second hit in my Google results…

    Shows B being subtracted from A before that value is multiplied by C. It's not distribution. It's evaluating the parenthetical.

    It’s -3 - where’s the trouble?

    The fact it's 3 and -6, not 3 - 6. Which is why I explicitly mentioned that -6 was a number, and used two other examples with -6. I wasn't just making conversation. Jesus fucking Christ, a state trusts you with the education of children.

    According to the textbook you're now screenshotting at people, A(B) and (B)A are both correct - yes? They're both valid? And spaces have no impact on an equation? And writing equations like -6 + 1 are fine, instead of (-6) + 1, since you don't want needless parentheses?

    • ‘this particular notation is the notation!’ to ‘of course other notations exist’

      The notation for division in some countries is the obelus, in other countries it's a colon. Whatever country you're in, the notation for that country is the notation for division (be it an obelus or a colon).

      Maths,” do you mean the notation on paper, or the underlying laws-of-reality stuff

      Both! Whatever notation your country uses, all the rules for Maths and use of that Maths notation are defined.

      It’s ambiguous

      No, it's not.

      It’s not distribution. It’s evaluating the parenthetical

      And Distribution applies to brackets/parentheses where they have a coefficient. In other words, same same.

      it’s 3 and -6, not 3 - 6

      You didn't put a comma between 3 and -6, so no, it's not 3 and -6, it's 3-6. That's what you wrote, that's what it is.

      a state trusts you with the education of children

      Related - have you noticed how children never get this wrong? It's only adults who've forgotten the rules of Maths who get it wrong.

      According to the textbook you’re now screenshotting at people, A(B) and (B)A are both correct - yes? They’re both valid? And spaces have no impact on an equation? And writing equations like -6 + 1 are fine, instead of (-6) + 1, since you don’t want needless parentheses?

      Yes (though the latter is unconventional), yes (though the latter is unconventional), yes, yes (though unconventional - 1-6 is the conventional way to write that), yes, yes.

      • Again pointing straight at RPN: does the colon go between the operands, or after them? That too is notation. That too is negotiable.

        The parts of mathematics that are eternal and discovered are separate from the parts that are arbitrary and invented. We are talking almost exclusively about the latter.

        Both!

        It’s ambiguous

        No, it’s not.

        Do you read the things you write?!

        And Distribution applies to brackets/parentheses where they have a coefficient. In other words, same same.

        No.

        What?

        No!

        Do you even know what your argument is?

        The central point you spammed a dozen people with, here in this thread from last year, is an insistence that multiplying by a parenthetical is different from distribution. You explicitly said 2(3+1) and 2*(3+1) are not the same thing. So when your hot second of Google knowledge shows (3+1), *2, converted to RPN, you do not get to claim that's the same thing as distribution, goddammit!

        You didn’t put a comma between 3 and -6, so no, it’s not 3 and -6, it’s 3-6. That’s what you wrote, that’s what it is.

        No, dumbass, (3) -6 is the quantities 3 and -6 in the format (A)B. A format you go on to say is fine with zero reflection or recognition, because you're experiencing this conversation one sentence at a time and putting absolutely zero thought into context or meaning.

        I fucking hated teachers like you. You're not listening. You're just preaching.

        • multiplying by a parenthetical is different from distribution

          Ok, let's tweak it (I've practically never used RPN, but only took me a couple of minutes of research to work it out)...

          1/2x3 same as 1 2 ÷ 3 x

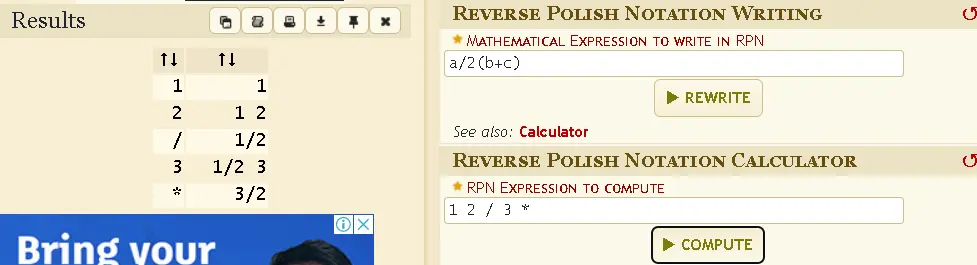
          1/2(3) same as 1 2 3 x ÷

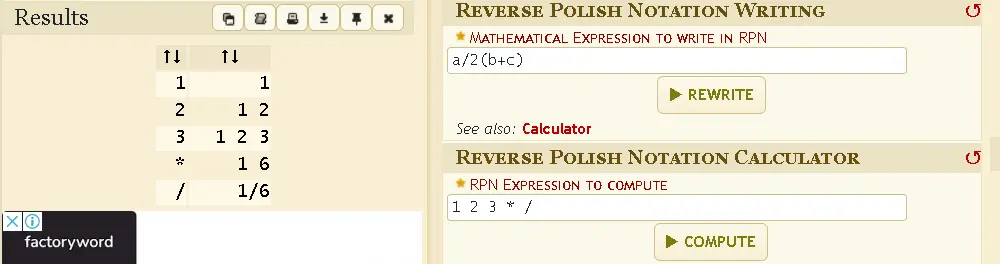
          ...and to bring it back to the original question...

          8/2x(2+2)

          8/2(2+2)

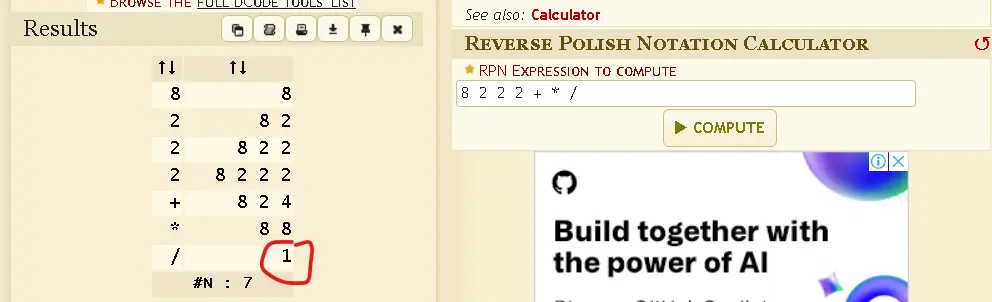
          Learn something new every day, :-) and took me no time at all to debunk your claim that it's not possible in RPN.

          (3) -6 is the quantities 3 and -6 in the format (A)B

          And what do you do with these "quantities"? Multiply them? If so then it's exactly the same as A(B). If you're talking about something else then tell me what you're talking about.

          zero thought

          I managed to work out how to do distribution in RPN, something you claimed couldn't be done, so who's the one giving zero thought?

          • If so then it’s exactly the same as A(B). If you’re talking about something else then tell me what you’re talking about.

            I'm talking about how you said (A)B for A=3 B=-6 equals -3. By all means, tell me it's because you read it as 3 - 6, because that's my fucking point. The math is immutable. The syntax can be ambiguous.

            I managed to work out how to do distribution in RPN, something you claimed couldn’t be done, so who’s the one giving zero thought?

            You don't understand the claim. No shit RPN can perform the individual steps of working through (A+B)C. But that equation does not exist in RPN. If you insist even (A+B)C is a different equation, then obviously ACBC+ is a different equation. You can do the math for distribution, using RPN, but the concept of distribution does not exist within RPN.

            You can't have rules about parentheses in a notation that does not have parentheses.

            What you did is only equivalent. In the exact same way that evaluating a parenthetical gets the same result as distribution. Because that part is math, not notation. And it doesn't matter if you do the multiplication using repeated addition, or the Russian peasant method, or floating point, or whateverthefuck. The math doesn't change... but many competing methods are equally valid.

            • I’m talking about how you said (A)B for A=3 B=-6 equals -3

              No, that's not what I said, since that's not what you said. You didn't write (A)B where A=3 and B=-6, you wrote (3)-6, which is 3-6 (the brackets are redundant as they are 2 terms separated by an operator), which is -3. If you intended this to be interpreted as a single term then you should've written (3)(-6), which is -18. Alternatively, if you had written (3)6, that would be equal to 18, but you wrote (3)-6, which is 2 terms separated by a minus. You wrote (A)-B, not (A)B (or (A)(B)), and so I read it as (A)-B.

              The syntax can be ambiguous.

              No, it's not. Now that I know what you mean, you just failed to write it the way you apparently intended - you didn't follow the syntax rules for multiplying by a negative.

              but the concept of distribution does not exist within in RPN

              So what you're really saying, as far as I can tell, is brackets themselves don't exist in RPN.

              evaluating a parenthetical gets the same result as distribution

              Except when it doesn't, which is my original point.

574 comments